Rethinking of Diffusion Model
摘要
从 VAE 原理出发,从数学角度推导扩散模型的 ELBO 和优化目标的来龙去脉。用三种方式(原始数据、噪声和分数)改写优化目标 ELBO 的去噪匹配项,解释 DDPM 为什么要使用学习噪音的方式建模扩散模型。
生成模型
对于我们感兴趣的某一分布
生成模型的几个大分类:
- GANs:基于对抗训练
- Likelihood-based:基于似然函数,包括 AE、flow、VAE 等
- Energy-based:基于能量函数
- Score-based:把优化能量函数的问题转换成优化分数(score)
从 VAE 开始
对于样本

最大化 ELBO 的原因有以下两点:
- 式子 16 说明了 ELBO 是似然的下界。
- 式子 15 说明:
。 关于 是常数,最大化 ELBO 等价于最小化 KL 散度,也就意味着我们可以用 $q\phi(z|x) p\theta(z|x)$ 。 因为
,当固定 时, 的值是不变的。调节 $q\phi(z|x) q\phi(z|x) p_\theta(z|x)$。
由此设计出如下的变分自编码器 VAE 结构,和 AE 隐变量是一个固定值不同,VAE 的 z 确切地说是隐空间。Encoder 中 x 通过预估的后验分布 $q\phi(z|x)
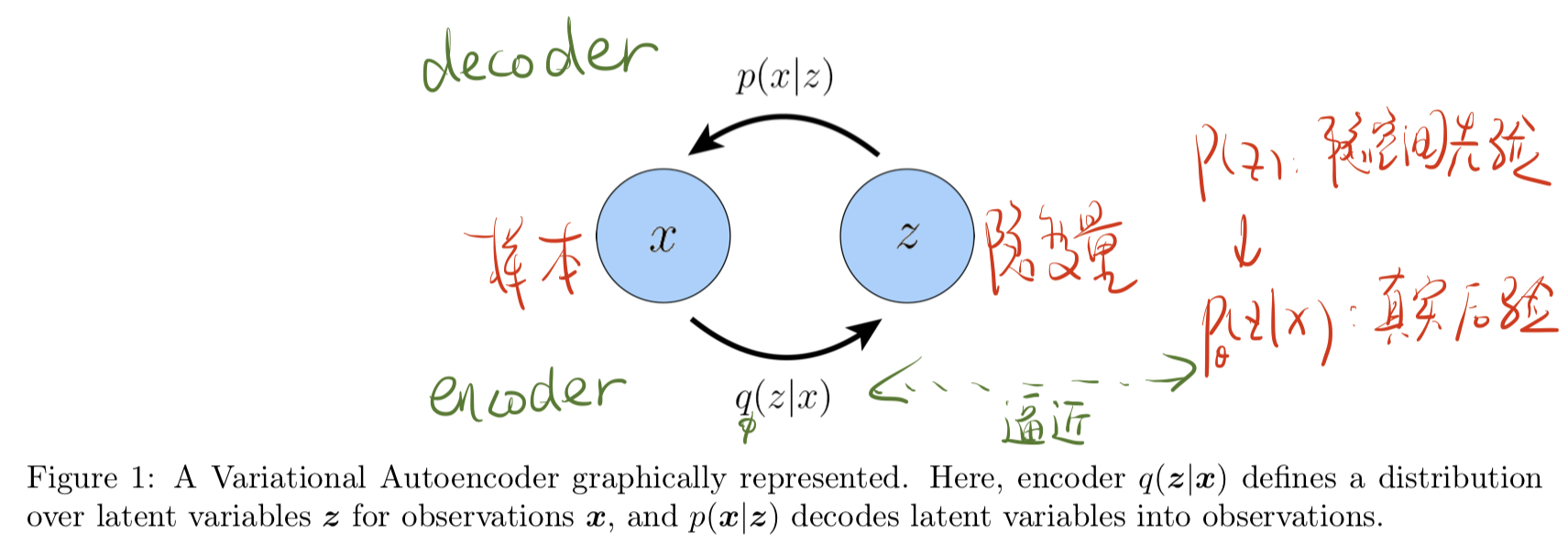
ELBO 可以写成两项之和,最大化 ELBO 就等于最大化它的第一项,最小化它的第二项。
- 第一项衡量 decoder 在变分分布中的似然,这确保了根据学习到的隐变量 z 的分布可以重建出原始 x 的分布。
- 第二项衡量的是 encoder 学到的变分分布保持了多少隐变量的先验信息
。减少这项鼓励编码器实际学习分布,而不是分解成狄拉克函数。

假设隐空间先验分布 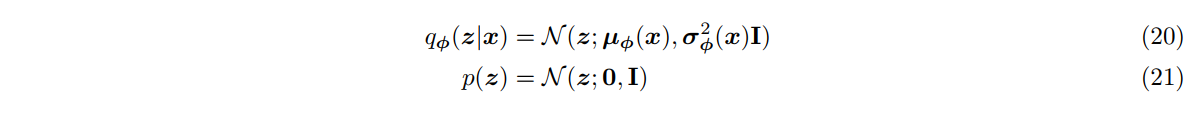
ELBO 的第二项 KL 散度可以直接计算。第一项用蒙特卡洛估计,先从分布 $q\phi(z|x)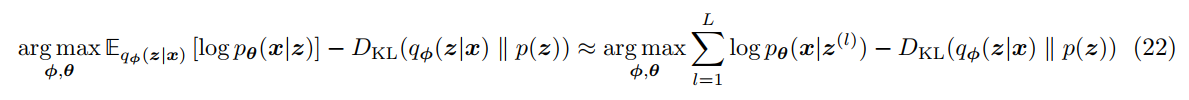
上式的第一项也可以理解为在给定 z 的时候,decoder 重构得到 x 的

分层 VAE(HVAE)
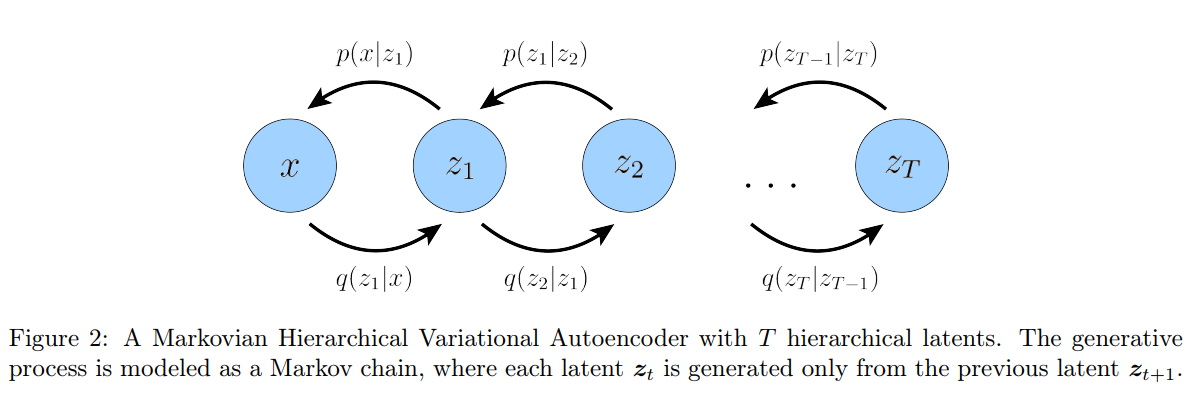
考虑分层 VAE 的一种特殊情况,称之为马尔可夫 HVAE (MHVAE)。在 MHVAE 中,生成过程为马尔可夫链,也就是说,解码每个隐变量 $zt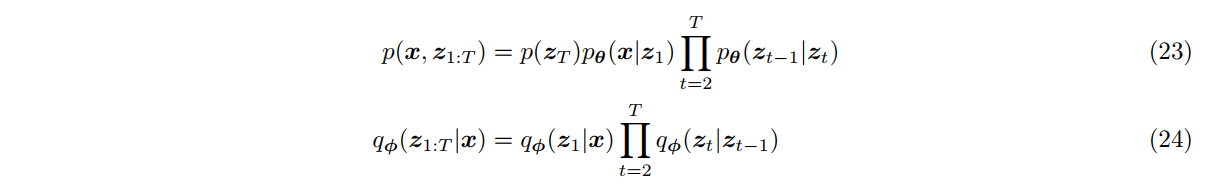
此时可以对优化目标 ELBO 进行形式上的推广,在下一章变分扩散模型 VDM 中,将会把其分解为几个特定项之和。
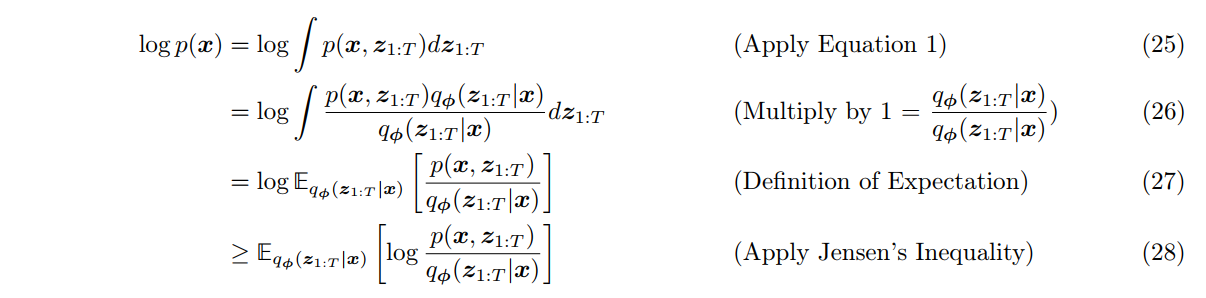
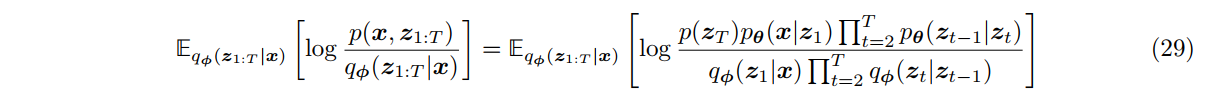
Variantional Diffusion Model
在分层 VAE 基础上添加三个条件:
- 潜变量 z 的维度和数据 x 保持一致。
- 每步的 encoder 固定为线性高斯模型,只依赖于上一个时间步的结果(马尔科夫条件)。意味着后验分布不再是由参数
决定,而是由上一个时间步决定均值和方差的高斯分布: - 最终时刻的隐变量分布为标准高斯分布。
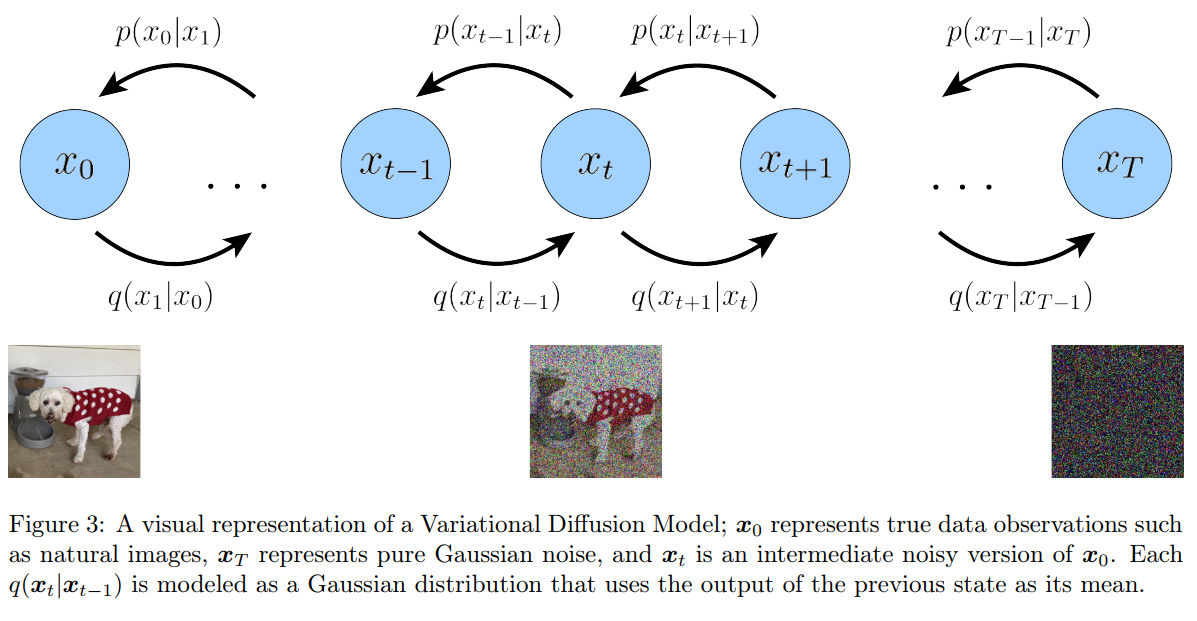
不同于 VAE 模型需要学习 encoder 和 decoder,对于 VDM 模型,只需要学习 decoder $p\theta(x{t-1}|xt)
ELBO
对于 VDM 模型,在式 29 基础上对 ELBO 进行形式上的扩展:
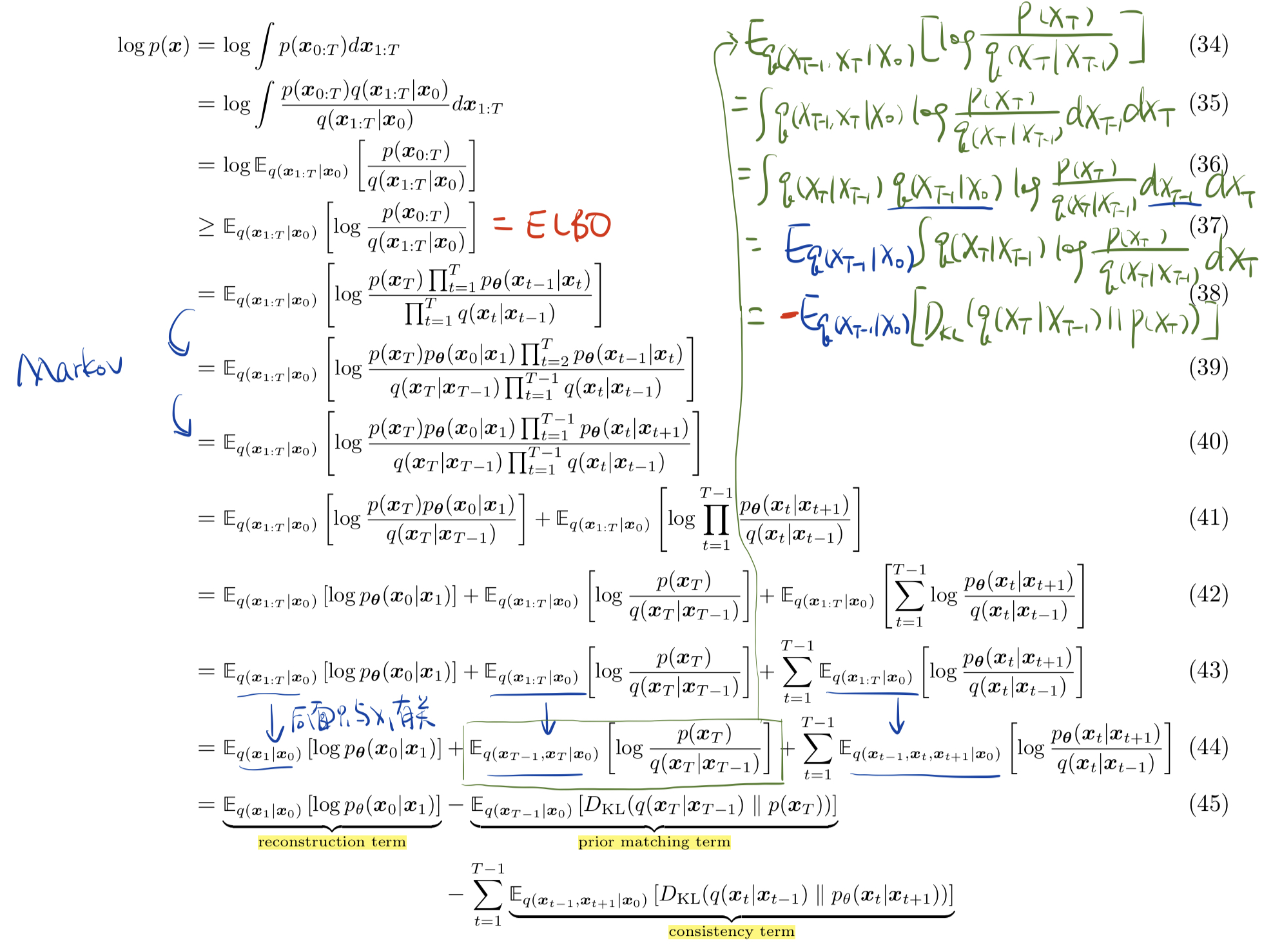
ELBO 最终分解为三项,它们的意义分别如下:
- Reconstruction term:通过第一层
重建得到的 对数似然尽量大。 - Prior matching term:使得最后一层的 q 分布趋近于
的先验分布,即标准高斯分布。注意到由于 q 分布都是预先设定的,因此这一项事实上不用优化,且在 T 足够大时保持为 0. - Consistency term:对于中间每一层的 $xt
q(x_t|x{t-1}) p\theta(x_t|x{t+1})$ 得到的结果一致,也就是最小化这两个分布的 KL 散度。
对于 ELBO 的三项表达式,由于都是期望的形式,可以用蒙特卡洛法结合重参数化进行计算(参考 VAE 中式 22 的处理方式)。但是第三项 consistency term 与两个随机变量 $x{t-1}
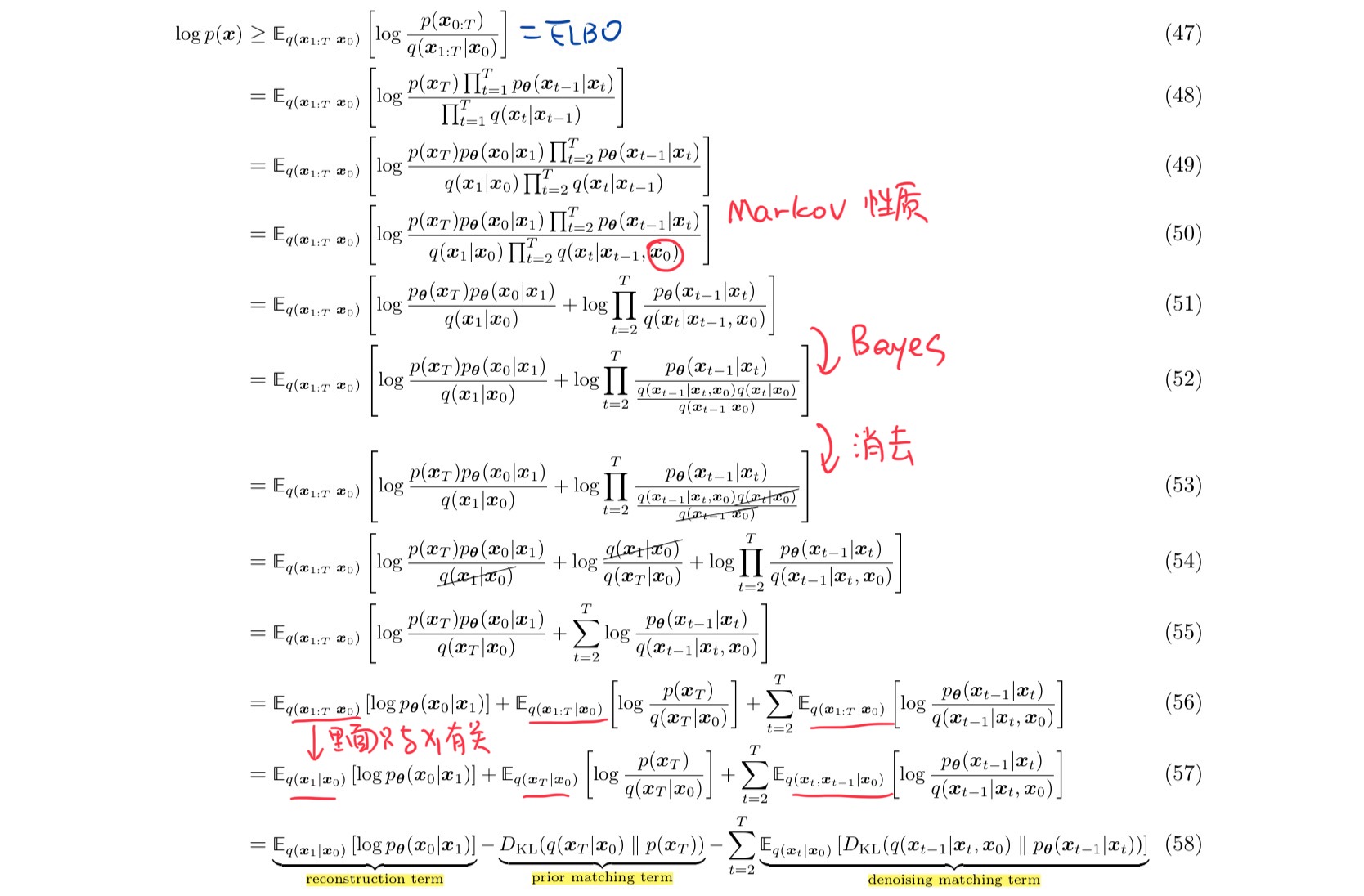
同样将 ELBO 最终分解为三项,它们的意义分别如下:
- Reconstruction term:通过第一层
重建得到的 对数似然尽量大。 - Prior matching term:使得最终的 q 分布趋近于
的先验分布,即标准高斯分布。注意到由于 q 分布都是预先设定的,因此这一项事实上不用优化,且在 T 足够大时保持为 0. - Denoising matching term:后验分布 $q(x{t-1}|x_t,x_0)
p\theta(x_{t-1}|x_t)$ 理解为要拟合的去噪分布,去噪匹配项的目标就是最小化两者的 KL 散度,使两个分布逼近。
注意到以上两种 ELBO (式 45 和式 58)的推导仅使用到了马尔可夫性质,因此对于任意 MHVAE 都适用。而 VDM 比通常的 MHVAE 多了 三条限制,导致 q 分布是已知的,这是两者主要的区别。另外,当 T=1 时,VDM 就退化为了普通的 VAE,ELBO 的形式也退化为 VAE 的形式(式 19)。
总结对 ELBO 的形式上的拆分,我们发现最大化 ELBO 这一优化目标最终成为了最小化 Denoising matching term,即去噪匹配项,这也是整个扩散模型的核心。后面我们将对去噪匹配项进行进一步变换,转换为对其他形式参数的优化,从而让神经网络进行学习。
去噪匹配项
首先对于真实的后验分布

回顾我们的最终目标:最小化去噪匹配项。真实后验分布 q 已经求得,现在处理要拟合的去噪分布 $p\theta(x{t-1}|xt)

使用神经网络预测得到 $\mu\theta
下面给出了模型在任意时刻 t 上建模的三种方式:直接预测原始数据 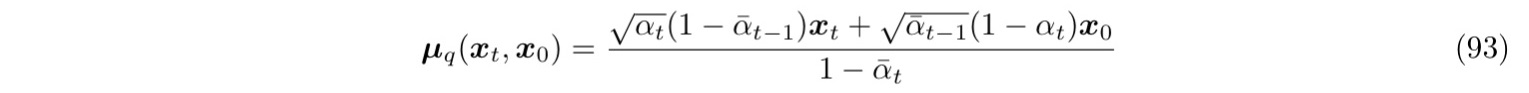
预测原始数据
第一种直接的想法是,把式 93 的 $x0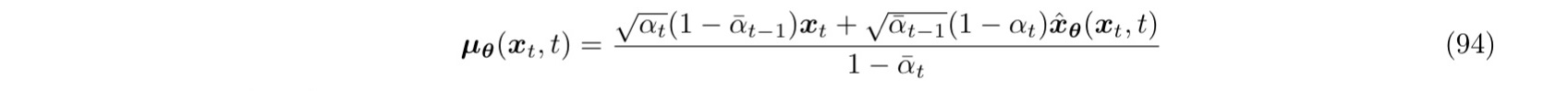
由 93 94 代入式子 92 就能得到优化目标: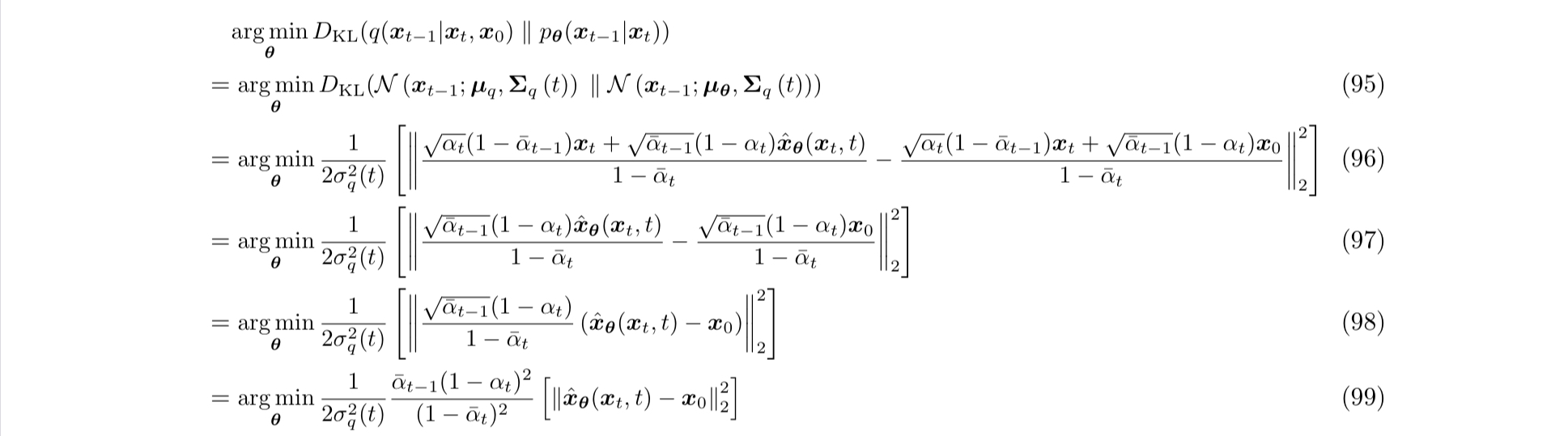
预测噪声
第二种方式,使用重参数化技巧把 
注意,上面的 $\epsilon0
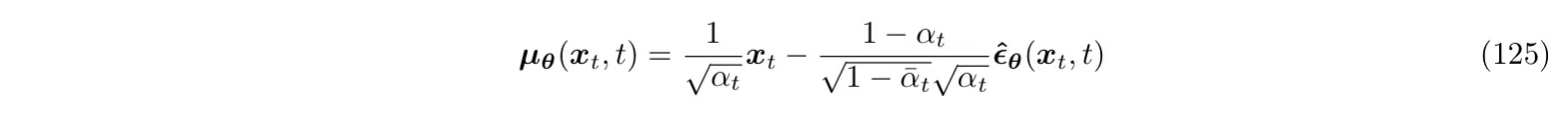
类似地,优化目标就成了最小化 
预测分数
第三种方式,首先通过 Tweedie’s Formula,把

模仿 $\muq
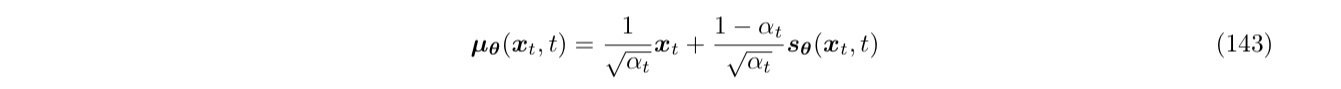
类似地,优化目标就成了最小化模型预测的分数和真实分数的距离。