论文精读 DDPM
摘要
2020 年 6 月,Jonathan Ho 等学者对之前的扩散概率模型进行了简化,并通过变分推断,将后验问题转为优化问题进行建模,提出了经典的去噪扩散概率模型(DDPM),将扩散概率模型的思想用于图像生成,目前所说的扩散模型,大多是基于该模型进行改进。
简单来说,DDPM包括两个过程:正向过程和逆向过程。
正向过程用 $q(xt|x{t-1})$ 表示,理解为以固定方式添加噪声,破坏原有的数据分布。
逆向过程用 $p\theta(x{t-1}|x_t)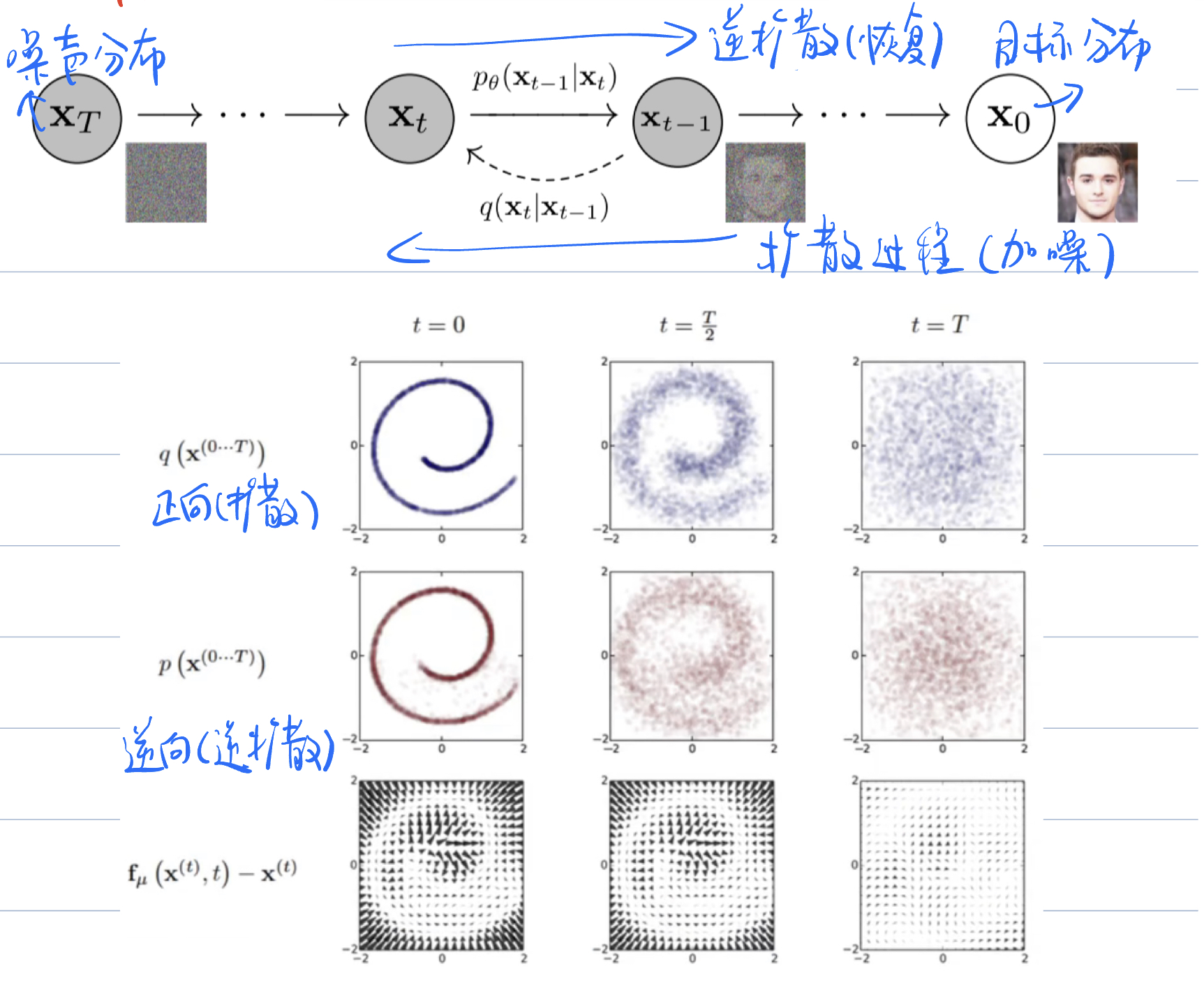
正向过程
从真实数据分布
由于每个时间步相对独立,因此是一个马尔科夫链过程,这是下面推导的重要前提。
下面基于


反向过程
整体上是一个去噪的过程,根据真实分布 $q(x{t-1}|x_t)
假设真实分布
下面推导后验条件概率: 
优化目标是使得神经网络估计的分布和后验条件分布越接近越好,KL 散度计算推导,详见 Rethinking of Diffusion Model。最终的优化目标是使两者的均值最为接近,进一步重参数化变成估计噪声。
流程


注意点
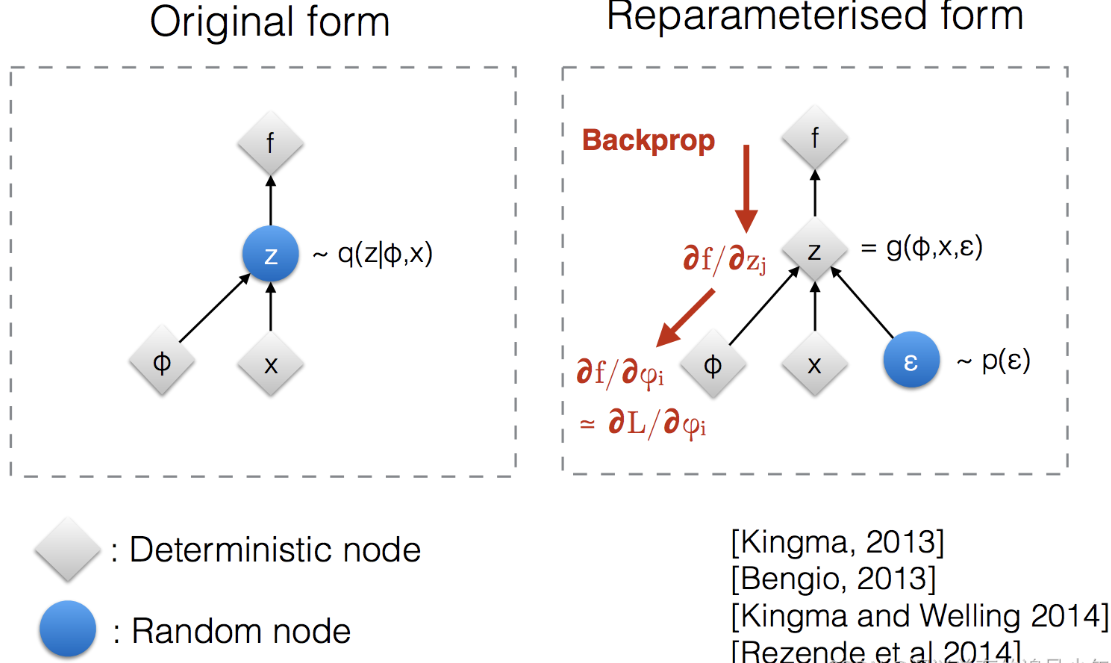
- 重参数化 使不可微的从分布中采样这一过程转化成了可微过程,从而反向传播。
的选择 使用Linear schedule加噪方式, , ,且 随着t递增。
代码演示
- 正向加噪过程

- 经过4000 轮训练后,反向生成结果
